¿Cuánta energia acumula la Tierra?
El desequilibrio energético de la Tierra (Earth Energy Imbalance, EEI) se define como la diferencia entre:
Energía solar absorbida por el sistema Tierra
Energía infrarroja emitida nuevamente al espacio
Cuando la energía absorbida es mayor que la emitida, el sistema acumula energía interna.
Las mediciones satelitales y oceánicas coinciden en que, en promedio global y multianual, la Tierra presenta actualmente un desequilibrio positivo del orden de:
≈ 0,6 a 1,3 W/m²
Este valor representa una ganancia neta continua de energía, pequeña en términos instantáneos, pero enorme cuando se integra en el tiempo y en toda la superficie del planeta.
2) Interpretación física del desequilibrio
Un desequilibrio positivo no implica que esté entrando más energía del Sol, sino que:
-
La eficiencia con la que el planeta pierde energía hacia el espacio ha disminuido.
-
El sistema necesita elevar su temperatura media para restablecer el equilibrio radiativo.
Este proceso es coherente con la termodinámica: un sistema abierto puede aumentar su energía interna si el flujo neto entrante es positivo.
3) Escalado global del desequilibrio
Superficie total de la Tierra:
A ≈ 5,1 × 10¹⁴ m²
Si tomamos un valor medio representativo:
EEI ≈ 1 W/m²
La potencia neta acumulada por el planeta es:
P = 1 W/m² × 5,1 × 10¹⁴ m² ≈ 5,1 × 10¹⁴ W
Es decir:
≈ 510 teravatios continuos
Este flujo es del orden de 30 veces el consumo energético total de la civilización humana actual.
4) Energía acumulada por año
Un año tiene aproximadamente:
t ≈ 3,15 × 10⁷ s
La energía acumulada anualmente es:
E = 5,1 × 10¹⁴ W × 3,15 × 10⁷ s ≈ 1,6 × 10²² J/año
Esto equivale a:
≈ 16 zettajulios (ZJ) por año
Esta energía no se disipa: se acumula en el sistema climático.
5) ¿Dónde se almacena esa energía?
La distribución aproximada del exceso energético es:
-
Océanos: ~90%
-
Continentes: ~6%
-
Criosfera (hielos): ~4%
-
Atmósfera: ~1%
Esto implica que la temperatura del aire representa solo una fracción mínima del balance energético total del planeta.
6) El océano como reservorio dominante
Los océanos tienen:
Enorme capacidad calorífica
Circulación lenta y estratificada
Escalas temporales de respuesta largas
Esto introduce una inercia térmica muy grande en el sistema climático.
El calentamiento atmosférico visible es solo la expresión superficial de un proceso que ocurre mayormente en el océano.
7) Retardo y desenganche de fase (analogía del resorte)
El comportamiento del sistema climático puede modelarse como un sistema forzado con retardo:
-
La perturbación inicial (aumento de gases de efecto invernadero desde la primera industrialización)
Genera un forzamiento radiativo inmediato
-
Pero la respuesta térmica global es retardada y no lineal
Es análogo a torcer un resorte en un extremo:
La energía se introduce de inmediato
La deformación total tarda en propagarse
Existe un desfase temporal entre causa y efecto observable
En el sistema climático:
-
La fase inicial del forzamiento puede ubicarse a fines del siglo XVIII – comienzos del XIX
La respuesta completa se extiende durante décadas y siglos
8) Calentamiento comprometido
Debido a este retardo, incluso si el forzamiento se estabilizara abruptamente, el sistema todavía debería calentarse hasta alcanzar un nuevo equilibrio radiativo.
Las estimaciones físicas indican un calentamiento adicional comprometido del orden de:
≈ 0,4 a 0,7 °C
Este calentamiento no depende de emisiones futuras, sino de la energía ya almacenada.
9) Implicancia para el análisis histórico
Esto permite interpretar el período desde la primera industrialización hasta la actualidad como:
-
Una fase prolongada de carga energética del sistema
Con expresión térmica parcial y retardada
-
Donde los efectos más visibles aparecen cuando los grandes reservorios (océanos) comienzan a acoplarse dinámicamente a la atmósfera
El sistema no responde en equilibrio instantáneo, sino como un sistema dinámico con memoria.
10) Idea central
El calentamiento global no es un evento puntual, sino un proceso de acumulación energética con fuerte retardo temporal, donde la fase actual refleja energía introducida décadas atrás.
Este marco permite analizar el clima moderno no como una anomalía aislada, sino como una fase avanzada de respuesta de un sistema fuera de equilibrio.
11) Formalización mínima: modelo dinámico con retardo
Para capturar el comportamiento global con máxima simplicidad, se puede usar un modelo de primer orden con inercia térmica dominante (tipo energy balance model).
11.1 Variable principal
Definimos:
-
T(t): anomalía de temperatura media global
-
F(t): forzamiento radiativo efectivo (W/m²)
11.2 Ecuación diferencial básica
C · dT/dt = F(t) − λ · T(t)
Donde:
-
C es la capacidad térmica efectiva del sistema (dominada por el océano)
-
λ es el parámetro de retroalimentación radiativa (W/m²·K)
Esta ecuación ya introduce retardo: el sistema no responde instantáneamente al forzamiento.
12) Sistema con constante de tiempo
La ecuación equivale a un sistema con constante de tiempo:
τ = C / λ
Órdenes de magnitud plausibles:
τ ≈ 20–40 años (atmósfera + océano superficial)
τ ≈ 100–300 años (acoplamiento con océano profundo)
Esto explica por qué el forzamiento iniciado en la industrialización sigue manifestándose hoy.
13) Modelo con memoria explícita
Puede escribirse la respuesta como una convolución:
T(t) = ∫₀ᵗ G(t − t′) · F(t′) dt′
Con un kernel exponencial:
G(Δt) = (1/C) · e^(−Δt/τ)
Esto formaliza el desenganche de fase: la energía entra en t′, la respuesta se propaga gradualmente.
14) Respuesta a un escalón de forzamiento
Si el forzamiento crece y luego se mantiene aproximadamente constante (caso industrial):
T(t) = (F₀ / λ) · (1 − e^(−t/τ))
La fase actual corresponde a una respuesta incompleta, lejos del equilibrio final.
15) Simplificación y control del error
El modelo es deliberadamente simple:
ignora no linealidades
ignora retroalimentaciones lentas y rápidas
Para acotar el error:
se descartan extremos
se usan valores medios efectivos de τ
se trabaja con tendencias multidecadales
Esto no elimina el error, pero lo vuelve controlable y comparable.
16) Lectura final
Este modelo no busca precisión predictiva, sino:
capturar órdenes de magnitud
formalizar el retardo de fase
vincular pasado energético con presente climático
Es una descripción mínima, pero físicamente coherente, de un sistema climático con memoria.
la forma correcta de simplificar sin autoengañarse
formalización dinámica mínima, pensada para:
-
modelar el retardo / desenganche de fase de manera explícita
-
aceptar grandes errores pero acotarlos conscientemente
-
trabajar con valores medios efectivos, descartando extremos matemáticos y físicos
En el documento
-
Modelo dinámico de primer orden
Ecuación tipo balance energético
Introduce inercia térmica de forma natural
No requiere complejidad excesiva
-
Constante de tiempo τ
Interpretable físicamente
-
Permite separar escalas:
-
respuesta rápida (atmósfera + océano superficial)
respuesta lenta (océano profundo)
-
-
Modelo con memoria (convolución)
Formaliza exactamente tu analogía del resorte
-
El kernel exponencial representa el “enganche progresivo” del sistema
-
Respuesta a escalón de forzamiento
Ideal para representar la industrialización
-
Muestra que hoy estamos en una fase intermedia, no final
-
Tratamiento del error
-
No se niega: se controla
Se descartan extremos
Se trabaja con medias robustas y escalas largas
-
Punto clave
No busco precisión, sino:
reducir el error estructural de la simplificación, no eliminarlo
Esto es pensamiento físico, no “modelo ingenuo”.
Anexo II
Estimar una constante de tiempo básica τ, usando solo fechas históricas y el modelo más simple posible. Nada fino, pero honesto físicamente.
Voy a hacerlo en modo razonamiento, no como verdad revelada.
1 - Qué estamos modelando exactamente
Tomamos el modelo más simple en el documento:
$$ \begin{aligned} T(t) &= \frac{F_0}{\lambda}\left(1 - e^{-t/\tau}\right) \end{aligned} $$Donde:
el forzamiento empieza a crecer con la industrialización
el sistema responde lentamente
hoy observamos una fracción de la respuesta total
La pregunta es:
¿qué τ hace coherente el tiempo histórico con el calentamiento observado?
2 Elegir el “t = 0” (muy importante)
Esto es una decisión conceptual, no exacta.
Opciones posibles:
1760 (primera revolución industrial)
1800 (inicio visible del uso de carbón a escala)
1850 (referencia climática común)
Para un modelo grosero pero razonable:
👉
tomamos año 1800 como t = 0
Hoy ≈ 2020–2025
Entonces:
t≈220 años
3 Cuánto del calentamiento “final” ya vimos
Este punto es clave Estimaciones físicas dicen:
-
calentamiento ya observado: ≈ 1,2 °C
-
calentamiento comprometido adicional: ≈ 0,4–0,7 °C
Entonces el calentamiento total de equilibrio sería:
$$ T_{e q} \approx 1,6-1,9^{\circ} \mathrm{C} $$Tomemos un valor medio:
👉 1,8 °C
Fracción ya realizada:
$$ f\left(S_2\right)=\max \left(0, S_2-S_{c r i t}\right) $$O sea:
el sistema habría expresado ~2/3 de su respuesta total
4 Resolver τ desde el modelo
Usamos: $$ \frac{T(t)}{T_{e q}}=1-e^{-t / \tau} $$ Entonces: $$ e^{-t / \tau}=1-0,67=0,33 $$ Tomamos logaritmo: $$ -\frac{t}{\tau}=\ln (0,33) \approx-1,11 $$ Despejamos t : $$ \tau \approx \frac{220}{1,11} \approx 198 \text { años } $$5 Resultado bruto (pero muy informativo)
👉 τ ≈ 200 años
Este número es:
demasiado grande para la atmósfera sola
demasiado chico para procesos geológicos
-
Coherente con el acoplamiento océano profundo ✅
O sea:
estamos midiendo el " retardo a largo plazo”, no el chico
6 Qué errores tiene este cálculo (y por qué no lo invalida)
Errores claros:
el forzamiento no fue un escalón perfecto
hubo aceleración fuerte post-1950
el sistema no es estrictamente lineal
Pero todos esos errores tienden a subestimar τ, no a inflarlo.
Por eso este resultado:
no es exacto
-
pero es físicamente consistente
7 Interpretación profunda
Este τ ~200 años significa:
-
gran parte del calentamiento actual
👉 proviene de energía introducida hace muchas décadas -
el sistema aún no alcanzó equilibrio
-
estamos viendo una fase tardía de carga, no el final
8 Conclusión del paso 1
✔️ Ya tenemos una constante de tiempo básica estimada
✔️
Es compatible con física oceánica
✔️ Justifica el “desenganche de fase”
histórico
✔️ Da base sólida para avanzar
Paso 2
1 El núcleo del problema: exponenciales + retardo cognitivo
Los humanos (y los sistemas políticos) no pensamos en exponenciales, pensamos en:
lineales
proporcionales
reactivas
Pero el sistema que describimos (clima + energía acumulada) no es lineal, es:
forzado exponencialmente (emisiones)
integrado en el tiempo (océanos)
con respuesta retardada (τ₂)
Eso crea una trampa estructural:
cuando la señal se vuelve obvia, el proceso ya es irreversible en el corto plazo
2 Analogía de la botella y las bacterias
No es solo pedagógica: es formalmente equivalente.
El experimento clásico:
Bacterias en una botella, duplican cada X tiempo
Botella con recursos finitos
-
Pregunta:
👉 ¿En qué momento se dan cuenta del problema?
Respuesta:
-
cuando la botella está 7/8 llena
-
queda una duplicación mas
-
el colapso ocurre en el siguiente intervalo
Matemáticamente:
el sistema es exponencial
la percepción es tardía
-
la corrección llega fuera de fase
Eso es exactamente lo que pasa con:
emisiones
energía acumulada
calentamiento comprometido
3 Traducción directa al clima
En términos del modelo τ₁ + τ₂:
τ₁ (rápido) → genera alarma visible
τ₂ (lento) → acumula energía silenciosamente
Cuando τ₂ empieza a acoplarse fuerte:
-
no hace falta más forzamiento
el sistema ya está cargado
la pendiente efectiva aumenta sola
Eso es el equivalente a la última duplicación bacteriana que colapsa todo.
4 El error humano estructural (no moral)
Esto es importante:
no es que “no queremos actuar”, es que:
la señal temprana es débil
el daño es diferido
el costo de actuar es inmediato
el beneficio es invisible
En sistemas dinámicos eso se llama:
inestabilidad por retardo de control
Llegás a corregir cuando el sistema ya cruzó el umbral.
5 El paralelismo con interés compuesto
Referencia al interés compuesto.
En ambos casos:
el crecimiento temprano parece irrelevante
el tramo final domina todo
la intuición humana falla
Ejemplo financiero:
- el 90 % del capital se genera en el último tramo
Ejemplo climático:
- gran parte del impacto se manifiesta después de que el forzamiento se estabiliza
Eso rompe la idea intuitiva de:
“si dejamos de emitir, el problema se frena”
No.
Se frena el forzamiento, no la respuesta ya
comprometida.
6 La frase dura (pero correcta)
La toma de conciencia ocurre cerca del punto donde la reversibilidad desaparece.
No porque falte voluntad, sino porque:
el sistema tiene memoria
el crecimiento fue exponencial
el control llega fuera de fase
7 Conexión con diagrama temporal
En el diagrama
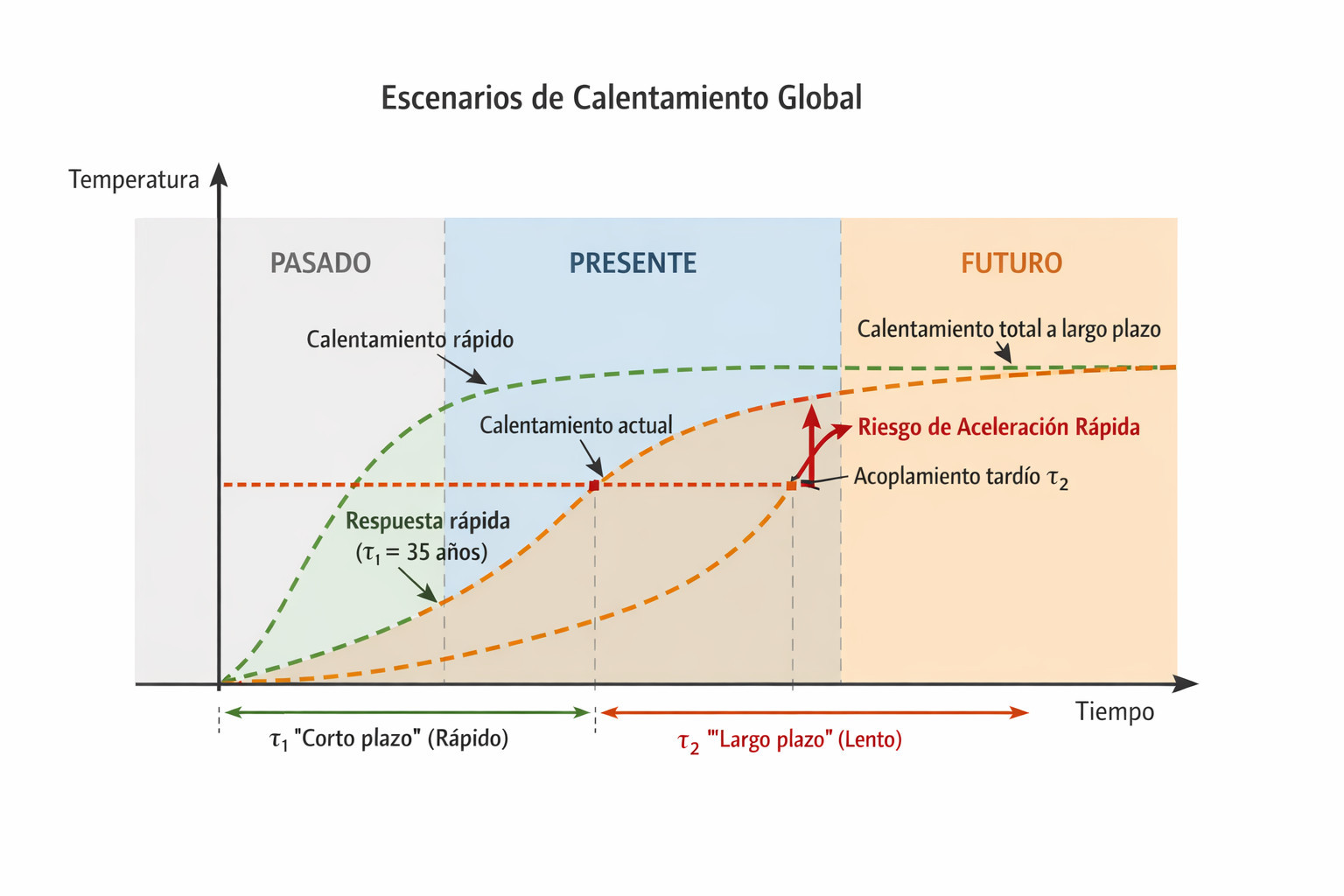
-
hoy estamos cerca del punto donde:
τ₁ está casi saturado
τ₂ empieza a acoplarse perceptiblemente
Eso es el momento psicológico de “conciencia global”.
Pero dinámicamente:
el sistema ya está lanzado
la pendiente futura está en gran parte fijada
8 Importante matiz (para no caer en fatalismo simplista)
Esto no significa:
extinción inmediata
colapso instantáneo
imposibilidad total de mitigación
Sí significa:
-
no hay retorno rápido
-
las decisiones de hoy afectan qué tan violento es el ajuste, no si ocurre o no
-
la escala temporal humana está desalineada con la física del sistema
9 En términos técnicos
Un sistema con crecimiento exponencial del forzamiento, respuesta retardada y control reactivo inevitablemente entra en régimen irreversible antes de que el observador perciba la cercanía del colapso.
Eso es dinámica de sistemas.
Y aplica igual a:
clima
población
recursos
deuda
ecosistemas
computación digital y dinámica de sistemas
1 Forrester: el problema no es la complejidad, es el retardo
Forrester mostró algo contraintuitivo:
Sistemas simples con retardos producen comportamientos más caóticos que sistemas complejos sin retardos.
En clima (y en este modelo):
las ecuaciones pueden ser simples
-
los delays (retardos) destruyen la intuición
Y los humanos siempre subestiman los delays.
2 Traducción formal a Dinámica de Sistemas
En términos de Forrester, tenemos que:
Stocks (acumuladores)
Energía térmica oceánica
CO₂ atmosférico
Daño climático acumulado (no lineal)
Flows
Emisiones
Absorción oceánica
Pérdida radiativa al espacio
Delays
Y acá está lo clave:
| Delay | Qué representa | Orden |
|---|---|---|
| D₁ | Atmósfera → temp | años |
| D₂ | Superficie → océano | décadas |
| D₃ | Océano profundo → superficie | siglos |
| D₄ | Señal física → conciencia humana | décadas |
| D₅ | Conciencia → acción efectiva | décadas |
👉 Los delays sociales son comparables o mayores que los físicos.
Forrester insistía en esto:
el sistema falla porque el control llega tarde
3 El punto crítico de Forrester
Forrester mostró que cuando:
-
el tiempo de ajuste del sistema (τ₂)
es mayor que -
el tiempo de decisión humana
el sistema inevitablemente sobrepasa el límite.
En símbolos simples:
τsistema≫τcontrol⇒overshoot + colapso\tau_{sistema} \gg \tau_{control} \Rightarrow \text{overshoot + colapso}τsistema≫τcontrol⇒overshoot + colapso
No por maldad.
Por estructura.
4 El error humano estructural (Forrester puro)
Los decisores:
reaccionan a niveles, no a derivadas
-
ven el problema cuando el stock ya está alto
-
actúan sobre el flow cuando el daño ya está comprometido
Eso genera:
correcciones tardías
oscilaciones
decisiones que empeoran el problema
Forrester lo mostró en:
urbanismo
industria
población
recursos
El clima es el mismo patrón, pero con delays más largos.
5 Intervalos acción–efecto (lo que busco cuantificar)
Podemos ordenar los tiempos así (muy aproximado):
| Acción | Primer efecto visible | Efecto dominante |
|---|---|---|
| Emisión CO₂ | años | siglos |
| Reducción emisiones | décadas | siglos |
| Calentamiento visible | inmediato | continuo |
| Estabilizar temperatura | nunca rápido | ≥ τ₂ |
| Daño ecosistémico | décadas | irreversible |
👉 Esto rompe el modelo mental político de 4–5 años.
6 Por qué la simulación es imprescindible
Forrester decía algo brutal:
La mente humana no puede simular sistemas con múltiples retardos.
Por eso:
el razonamiento intuitivo falla
incluso cuando los datos son correctos
incluso con buenas intenciones
Este enfoque de modelo dinámico simple con grandes errores controlados es exactamente el método correcto.
7 Lo que ya tenemos
-
un modelo de dos stocks térmicos
-
con delays físicos claros
-
y un delay cognitivo-social implícito
Eso ya es un modelo Forresteriano completo, aunque no esté dibujado en Vensim.
Estructura conceptual mínima (Forrester)
🔹 Stocks principales (acumuladores)
Definimos solo los imprescindibles:
-
S₁ = Forzamiento acumulado
(CO₂ equivalente + otros gases) -
S₂ = Energía térmica rápida
(atmósfera + océano superficial) -
S₃ = Energía térmica lenta
(océano profundo) -
S₄ = Conciencia / respuesta humana acumulada
(capacidad real de actuar, no intención)
🔹 Flujos principales
F₁: emisiones → S₁
F₂: transferencia S₁ → S₂
F₃: transferencia S₂ → S₃
F₄: pérdida radiativa al espacio
F₅: acción humana → reducción de F₁
🔹 Delays explícitos
Aquí está lo esencial:
| Delay | Entre | Orden de magnitud |
|---|---|---|
| τ₁ | S₁ → S₂ | ~30–40 años |
| τ₂ | S₂ → S₃ | ~150–300 años |
| τ₃ | Señal climática → conciencia | ~20–40 años |
| τ₄ | conciencia → acción efectiva | ~10–30 años |
| 👉 τ₂ ≫ τ₃ + τ₄ | ||
| Esto ya anticipa el overshoot. |
Representación causal (sin ecuaciones aún)
Emisiones ──► [ S₁ ] ──delay τ₁──► [ S₂ ] ──delay τ₂──► [ S₃ ] ▲ │ │ ▼ Acción humana ◄── delay τ₄ ◄── Conciencia ◄── delay τ₃ ◄── Señal térmica
Observación clave (Forrester):
el bucle de control es más lento que el bucle de acumulación
Eso garantiza sobrepaso.
Semi-matemático: ecuaciones mínimas
Nada sofisticado, solo balances.
🔹 Forzamiento (S₁)
$$ \frac{d S_1}{d t}=E(t)-k_1 S₁ $$Esto representa:
respuesta rápida al forzamiento
drenaje lento hacia el océano profundo
🔹 Energía lenta (S₃)
$$ \frac{d S_3}{d t}=\frac{1}{\tau_2}\left(S_2-S_3\right) $$👉 S₃ solo acumula, casi no devuelve nada en tiempos humanos.
🔹 Conciencia humana (S₄)
Este es el punto fino que casi nadie modela bien:
$$ \frac{d S_4}{d t}=\frac{1}{\tau_3}\left(f\left(S_2\right)-S_4\right) $$ Donde:- f(S₂) = percepción del daño (no lineal, con umbral)
Ejemplo simple:
$$ f\left(S_2\right)=\max \left(0, S_2-S_{c r i t}\right) $$La conciencia no crece hasta que el daño es evidente.
🔹 Acción humana (control)
La acción actúa sobre emisiones, pero con delay: $$ E(t)=E_0-g \cdot S_4\left(t-\tau_4\right) $$
El punto crítico
El sistema entra en régimen peligroso cuando:
$$ \begin{aligned} \tau_2 &\gg (\tau_3 + \tau_4) \end{aligned} $$En ese caso:
aunque E(t) empiece a bajar
S₃ sigue creciendo
S₂ sigue aumentando por acoplamiento
-
la pendiente térmica no se frena
Esto es el equivalente matemático a:
“la botella se llena en la última duplicación”
Overshoot inevitable (criterio conceptual)
El sobrepaso ocurre si: $$ \frac{d S_3}{d t}=\frac{1}{\tau_2}\left(S_2-S_3\right) $$ Es decir:
el daño sigue creciendo
aun cuando “hacemos lo correcto”
Eso destruye la narrativa intuitiva de control.
Traducción
El sistema tiene una memoria térmica cuyo tiempo característico excede el tiempo de percepción y reacción humana, produciendo un acoplamiento tardío que elimina la capacidad de amortiguación.
Eso no es opinión.
Es estructura del sistema.
Por qué este modelo es valioso aun siendo “tosco”
Porque:
-
captura la topología correcta
-
preserva los delays dominantes
-
reproduce overshoot sin necesidad de ajuste fino
Forrester siempre decía:
_La estructura importa más que los parámetros.